局部敏感哈希(Locality Sensitive Hashing,LSH)总结
什么是局部敏感哈希(Locality Sensitive Hashing,LSH)
说到Hash,大家都很熟悉,是一种典型的Key-Value结构,最常见的算法莫过于MD5。其设计思想是使Key集合中的任意关键字能够尽可能均匀的变换到Value空间中,不同的Key对应不同的Value,即使Key值只有轻微变化,Value值也会发生很大地变化。这样特性可以作为文件的唯一标识,在做下载校验时我们就使用了这个特性。但是有没有这样一种Hash呢?他能够使相似Key值计算出的Value值相同或在某种度量下相近呢?甚至得到的Value值能够保留原始文件的信息,这样相同或相近的文件能够以Hash的方式被快速检索出来,或用作快速的相似性比对。局部敏感哈希(Locality Sensitive Hashing,LSH)正好满足了这种需求,在大规模数据处理中应用非常广泛,例如已下场景
- 近似检测(Near-duplicate detection):通常运用在网页去重方面。在搜索中往往会遇到内容相似的重复页面,它们中大多是由于网站之间转载造成的。可以对页面计算LSH,通过查找相等或相近的LSH值找到Near-duplicate。
- 图像、音频检索:通常图像、音频文件都比较大,并且比较起来相对麻烦,我们可以事先对其计算LSH,用作信息指纹,这样可以给定一个文件的LSH值,快速找到与其相等或相近的图像和文件。
- 聚类:将LSH值作为样本特征,将相同或相近的LSH值的样本合并在一起作为一个类别。
首先来看LSH的图形化解释:

左图是传统Hash算法,右图是LSH。红色点和绿色点距离相近,橙色点和蓝色点距离相近。
- 传统Hash算法,得到的value值完全不一样
| 绿色点 1 0 0 0 0 0 0 0 | 红色点 0 0 0 0 1 0 0 0 |
| 橙色点 0 1 0 0 0 0 0 0 | 蓝色点 0 0 0 0 0 0 0 1 |
- LSH算法,红色点和绿色点的value值相等,橙色点和蓝色点的value值相近。
| 绿色点 0 0 1 0 0 0 0 0 | 红色点 0 0 0 0 0 1 0 0 |
| 橙色点 0 0 1 0 0 0 0 0 | 蓝色点 0 0 0 0 0 0 1 0 |
维基百科对LSH的解释:LSH有几种不同的定义形式,不过还是大牛Charikar的定义相对简单明了: 对于两个物体$\boldsymbol u, \boldsymbol v$(可以理解为两个文件、两个向量等),LSH生成的value值的每一bit位相等的概率等于这两个物体的相似度,表示为数学形式就是下式:
$$Pr_{h \in H}[h(\boldsymbol u)=h(\boldsymbol v)] = \phi(\boldsymbol{u,v})$$
等式左边表$Pr_{h \in H}[h(\boldsymbol u)=h(\boldsymbol v)]$示$\boldsymbol u, \boldsymbol v$两个物体Hash后的value值$h(\boldsymbol u),h(\boldsymbol v)$相等的概率。等式右边$\phi(\boldsymbol{u,v})$表示两个物体$\boldsymbol u, \boldsymbol v$的相似度(归一化到$[0,1]$)。这里不需要明确$\phi(\boldsymbol{u,v})$是什么度量方式(由此引申出了各种各样的LSH算法),只要满足上式的就叫做LSH。 显然这种定义天生就使LSH在hash后能够保留原始样本差异程度的信息,相近的物体的汉明距离就相近。有多相近呢?我们做一个简单的概率变换就能知道:设Hash后的value值有$n$比特,$\boldsymbol u, \boldsymbol v$两个物体有$x$位比特相等的概率就是
$$Pr\lbrace X=x \rbrace = C_n^x\phi(\boldsymbol u, \boldsymbol v)^x(1-\phi(\boldsymbol u, \boldsymbol v))^{n-x}$$
期望是多少呢?
$$\Bbb E(x) = n\phi(\boldsymbol u, \boldsymbol v)(二项分布的期望)$$
就是有$\phi(\boldsymbol u, \boldsymbol v)$位比特相等,这个结果是不是很漂亮呢?
局部敏感哈希的实现
前面讲了LSH的定义,下面进入实现部分,我们将按LSH的发展顺序介绍几种应用广泛的LSH算法。
基于随机投影的方法:
基于随机投影方法的LSH主要有两种——基于Stable Distribution的投影(http://www.slaney.org/malcolm/yahoo/Slaney2008-LSHTutorial.pdf)方法和基于随机超平面投影的方法。Tutorial是一篇较为容易理解的基于Stable Dsitrubution的投影方法的,有兴趣的可以看一下。其思想在于高维空间中相近的物体,投影(降维)后也相近。我们看下图,三围空间中的四个点,红色圆形在三围空间中相近,绿色方块在三围空间中相距较远,那么投影后还是红色圆形相距较近,绿色方块相距较远.
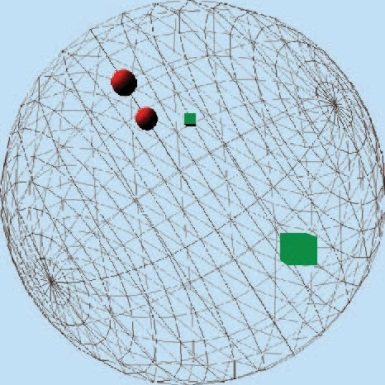
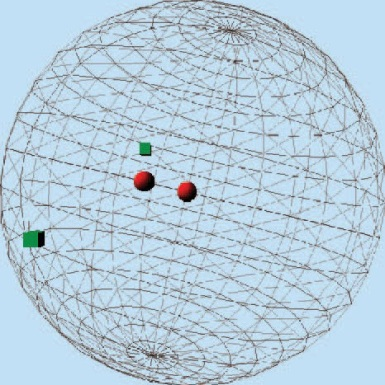
基于Stable Distribution的投影LSH,就是产生满足Stable Distribution的分布进行投影,最后将量化后的投影值作为value输出,具体数学表示形式如下: 给定特征向量$\boldsymbol v$,Hash的每一bit的生成公式为:
$$h(\boldsymbol v) = \lfloor\frac{\boldsymbol x \cdot \boldsymbol v + b}{w}\rfloor$$
其中,$\boldsymbol x$是一个随机数,从满足Stable Distribution的分布中抽样而来(通常从高斯或柯西分布中抽样而来)。$\boldsymbol x \cdot \boldsymbol v$就是投影(和单位向量的内积就是投影);$w$值可以控制量化误差;$b$是随机扰动,避免极端情况产生。我们通过下面的例子来了解这些参数是如何发生作用的: 还是上面的图形,假设红色圆形在$\boldsymbol x$方向上的投影是5和6,绿色方块在$\boldsymbol x$方向上的投影值是1和8(发生了$\boldsymbol x \cdot \boldsymbol v$操作)。这时,如果我们取$b=0,w=2.5$那么红色圆形就Hash在一起(Hash值为2),绿色方块Hash在了不同的位置上(哈希值为0和3),满足了相似物体Hash到一起,不相似的物体Hash不在一起的需求。但如果我们取$w=3$呢?这时绿色方块虽然没有Hash到在一起(Hash值为0和2),但红色圆形也没有hash到一起(Hash值为1和2)。怎么办呢?我们就可以通过$b$进行调节。为了防止这种情况一直发生,我们可以随机取$b=1$以增加扰动,这时红色圆形的Hash值就都为2了,而绿色方块的Hash值还是为0和2。 更详细的介绍在http://www.mit.edu/~andoni/LSH/上,理论看起来比较复杂,不过只要记住如果$\boldsymbol x$抽样于高斯分布,那么$\phi(\boldsymbol{u,v})$衡量的是L2 norm;如果$\boldsymbol x$抽样于柯西分布,那么$\phi(\boldsymbol{u,v})$衡量的是L1 norm。 这个就是LSH方法的鼻祖啦,缺点显而易见:你需要同时选择和两个参数,并且量化后的哈希值是一个整数而不是bit形式的0和1,你还需要再变换一次。如果要应用到实际中,简直让你抓狂。 不过大神Charikar改进了这种情况,提出了一种随机超平面投影LSH,这种方法Hash的每一bit的数学定义式为:
$$h(\boldsymbol v) = sgn(\boldsymbol x \cdot \boldsymbol v)$$
$\boldsymbol x$是随机超平面单位向量,sgn是符号函数
$$ sgn(x) = \begin{cases} 1, x \ge 0 \\ 0, x < 0 \\ \end{cases} $$
这时$\phi(\boldsymbol u,\boldsymbol v)$衡量的就是$\boldsymbol u$和$\boldsymbol v$的cosine距离:
$$Pr_{h \in H}[h(\boldsymbol u)=h(\boldsymbol v)] = \phi(\boldsymbol u,\boldsymbol v)=1 - \frac{\theta(\boldsymbol u,\boldsymbol v)}{\pi}$$
其中,$\theta(\boldsymbol u,\boldsymbol v)$表示向量$\boldsymbol u$和$\boldsymbol v$的夹角。 其根据在哪呢?我们来看下图
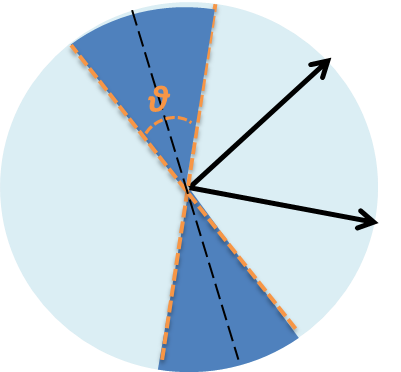
给定两个向量(图中的黑色箭头),只有在其法线的交叠区域(深蓝色区域)投影后的方向(sgn函数的值)才不相等,所以有$Pr_{h \in H}[h(\boldsymbol u)=h(\boldsymbol v)] =1 - \frac{\theta(\boldsymbol u,\boldsymbol v)}{\pi}$。 这种方法的最大优点在于: 1. 不需要参数设定 2. 是两个向量间的cosine距离,非常适合于文本度量 3.计算后的value值是比特形式的1和0,免去了前面算法的再次变化
SimHash
前面介绍的LSH算法,都需要首先将样本特征映射为特征向量v的形式,使得我们需要额外存储一个映射字典,难免麻烦,大神Charikar又提出了大名鼎鼎的SimHash算法,在满足随机超平面投影LSH特性的同时避免了额外的映射开销,非常适合于token形式的特征。
首先来看SimHash的计算过程http://gemantic.iteye.com/blog/1701101:
1,将一个f维的向量V初始化为0;f位的二进制数S初始化为0;
2,对每一个特征:用传统的hash算法(究竟是哪种算法并不重要,只要均匀就可以)对该特征产生一个f位的签名b。对i=1到f:
如果b的第i位为1,则V的第i个元素加上该特征的权重;
否则,V的第i个元素减去该特征的权重。
3,如果V的第i个元素大于0,则S的第i位为1,否则为0;
4,输出S作为签名。
下面我们通过一个实际的例子进行解释:
假设我的特征集合是{dog,cat,monkey},对应的权重为{1,2,3},假设需要生成f=3位的Hash值,生成过程如下:
用一个传统哈希算法得到特征对应的f=3位的Hash值:
假设传统Hash算法获得的对应key-value值如下:
hash(dog) = [1,0,1]
hash(cat) = [0,1,1]
hash(monkey) = [0,0,1]
按列求和,如果是1就做加法,如果是0就做减法,并乘以对应权重得到三列和值
红色列:1-2-3 = -4
绿色列:-1+2-3 = -2
蓝色列:1+2+3 = 6
做判别,得到01输出值 sgn(-4) = 0,sgn(-2) = 0,sgn(6) =1 因此得到的Hash值为001 这个算法是如何和与随机超平面投影LSH关联起来的呢? 我们可以将{dog,cat,monkey}表示为特征向量的形式,假设f1=dog,f2=cat,f3=monkey,结合对应的权重{1,2,3},表示为特征向量形式就是$v=[1,2,3]$。第2步按列求和过程相当于根据传统Hash值产生了三个随机向量x,然后与v做投影。这里三个随机向量为
$x_1=[1,-1,-1]$, $x_2=[-1,1,-1]$, $x_3=[1,1,1]$
不过需要注意的是,这里产生的超平面是退化的,每一维度上不是1就是-1,因此性能会有一定损耗。比如下面的极端情况:特征向量都在与坐标轴小于45°的区域时,SimHash后的value值都会相等。所以在选择特征权重时,如果某一维度权重过大就会使得其他维度的存在毫无意义,这是应该避免的情况。 Simhash为什么可以不用事先将样本特征映射为向量形式呢?这是因为投影向量的产生与特征相关联,内积计算里的乘法项可以保证对应项两两相乘;又注意到内积里做加法时是与顺序无关的,所以可以不用事先将样本特征映射为向量形式,省略了排序和查找的时间,极其巧妙,非常适合大规模数据处理。 Ps:引用SimHash的文章通常都标为这篇Similarity Estimation Techniques from Rounding Algorithms,但这篇文章里实际是讨论了两种metric的hash,引出自己的$Pr_{h \in H}[h(\boldsymbol u)=h(\boldsymbol v)]=\phi(\boldsymbol u,\boldsymbol v)$定义,我推测讲的SimHash应该是随机超平面投影LSH,而不是后来的token形式的SimHash,真是太坑爹了。。。
Kernel LSH
前面讲了三种LSH算法,基本可以解决一般情况下的问题,不过对于某些特定情况还是不行:比如输入的key值不是均匀分布在整个空间中,可能只是集中在某个小区域内,需要在这个区域内放大距离尺度。又比如我们采用直方图作为特征,往往会dense一些,向量只分布在大于0的区域中,不适合采用cosine距离,而stable Distribution投影方法参数太过敏感,实际设计起来较为困难和易错,不免让我们联想,是否有RBF kernel这样的东西能够方便的缩放距离尺度呢?或是我们想得到别的相似度$\phi(\boldsymbol u, \boldsymbol v)$表示方式。这里就需要更加fancy的kernel LSH了。 我们观察前面的几种LSH,发现其形式都可以表示成
$$threshold(\boldsymbol x \cdot \boldsymbol v + b)$$
用到的都是内积形式。提到内积不难想到kernel方法,是不是LSH也能使用kernel呢?也能使用下面的kernel形式呢?
$$Pr[threshold(\phi(\boldsymbol x) \cdot \phi(\boldsymbol u)+b)] = threshold(\phi(\boldsymbol x) \cdot \phi(\boldsymbol u)+b))=\Phi(\phi(\boldsymbol u),\phi(\boldsymbol v))$$
这样问题就转换为两个思考方向:1. 选定核空间,是否可以直接得到核空间中的$\phi(\boldsymbol u)$和核空间中的高斯变量$\phi(\boldsymbol x)$。2. 或是我们能够得到高斯变量$\phi(\boldsymbol x)$对应的$\boldsymbol x$,就可通过核函数变换计算$\phi(\boldsymbol x) \cdot \phi(\boldsymbol u)=K(\boldsymbol x,\boldsymbol u)$,即
$$Pr[threshold(K(\boldsymbol x,\boldsymbol u)+b)]=threshold(K(\boldsymbol x,\boldsymbol v)+b )]=\Phi(K(\boldsymbol u,\boldsymbol v))$$
Kernelized Locality-Sensitive Hashing for Scalable Image Search中通过半监督的方法,得到$\phi(\boldsymbol x) \cdot \phi(\boldsymbol u)$,避免了直接求取$\phi$函数,但是需要依赖于数据集的半监督训练,不适合大数据量处理。不过如果我们有$\phi(\boldsymbol x)$的有限维显式表示就可以不必这么麻烦,这就需要进几年发展迅速的kernel map技术:通常我么可以得到无限维的无损$\phi(\boldsymbol x)$,或是有限维的有损$\phi(\boldsymbol x)$。Locality-Sensitive Binary Codes From Shift-Invariant Kernels一文中巧妙设计了Hash函数$h(\boldsymbol v)$,避免了如何截断无限维$\phi(\boldsymbol x)$的问题和生成核空间高斯变量$\phi(\boldsymbol x)$的额外损耗,我们来看一下他是怎么做的: 首先先来了解一下什么是Shift Invariant kernel,其具有以下三个性质:
1. $K(\boldsymbol x,\boldsymbol y)=K(\boldsymbol x - \boldsymbol y)$
2. $K(\boldsymbol x-\boldsymbol y)\le1$ 并且 $K(x-x) \equiv K(0)=1$
3. 对任意实数$\alpha \ge 1, K(\alpha\boldsymbol x-\alpha\boldsymbol y) \le K(\boldsymbol x - \boldsymbol y)$
显然RBF kernel是这样的核函数,文章指出对于RBF kernel,存在一个显示变换
$$\phi(\boldsymbol x)=\sqrt2cos(\boldsymbol w \cdot \boldsymbol x + b)$$
其中$w$服从于均值为0,方差为$\sigma$的高斯分布$\mathscr N(0,\sigma\boldsymbol I)$,$b$服从于$[0,2\pi]$上的均匀分布,使得下式成立
$$\Bbb E[\phi(\boldsymbol x)\phi(\boldsymbol y)] = K(\boldsymbol x-\boldsymbol y)=K(\boldsymbol x,\boldsymbol y)$$
这样可以引出,也是文献Random Features for Large-Scale Kernel Machines中的结论
$$\Bbb E[\phi^n(\boldsymbol x) \phi^n(\boldsymbol y)]=K(\boldsymbol x-\boldsymbol y)=K(\boldsymbol x,\boldsymbol y)$$
$$\phi^n(\boldsymbol x)=\frac{1}{\sqrt n}(\phi_{w_1,b_1}(\boldsymbol x),…,\phi_{w_n,b_n}(\boldsymbol x))$$
相当于在概率意义下,$\phi^n(\boldsymbol x)$就是kernel Map,可以看作是显示映射。 这里有了Kernel Map,并且映射后值域是$[-\frac{\sqrt2}{\sqrt n},\frac{\sqrt2}{\sqrt n}]$,显然可以在核空间中计算$\phi(\boldsymbol x) \cdot \phi(\boldsymbol y)$,但问题在于上面的式子是在概率意义下相等,需要选择足够多的$n$,才能有较好的性能(自己小范围实验了以下,64位的性能已经不错)。文章并没有直接取核空间中的高斯变量$\phi(\boldsymbol x)$变化到核空间中,而是巧妙的定义了hash函数为以下形式
$$h(\boldsymbol v)=sgn(cos(\boldsymbol w \cdot \boldsymbol v + b) + t)$$
其中$t$抽样于均匀分布$[-1,1]$。 这样避免了$\phi^x(\boldsymbol x)$的$n$选择和额外生成高斯随机向量$\phi(\boldsymbol x)$的开销。 PS:文章里写的是
$$F(\boldsymbol v) = \frac12 [1+sgn(cos(\boldsymbol w \cdot \boldsymbol v + b) + t)]$$
原因是sgn函数用的不一样,文章里的sgn函数是判别到$[-1,1]$,而不是$[0,1]$
来看文章如何证明这个式子满足$Pr_{h \in H}[\phi(\boldsymbol u)=\phi(\boldsymbol v)]$
首先Lemma 2.1有
$$Pr[sgn(u+t) \ne sgn(v+t)]=\frac12 |u-v|$$
如下图,只有$t$落在红色区域时,sgn函数值才不想等

利用Lemma 2.1结论,Lemma 2.2证明
$$\Bbb E[h(\boldsymbol u) \ne h(\boldsymbol v)=\frac12\Bbb E[|cos(\boldsymbol w \cdot \boldsymbol u + b) - cos(\boldsymbol w \cdot \boldsymbol v + b)|]=\Bbb E[|sin(\frac{\boldsymbol w \cdot (\boldsymbol u - \boldsymbol v)}{2})sin(\frac{\boldsymbol w \cdot (\boldsymbol u + \boldsymbol v) + 2b}{2})|]$$
$\boldsymbol w$和$b$相互独立,所以可以先对$b$积分,得到下式
$$=\frac2\pi \Bbb E[|sin(\frac{\boldsymbol w \cdot (\boldsymbol u - \boldsymbol v)}{2})|]$$
这里有一个技巧:令$g(\tau)=|sin(\tau)|$,对其做傅立叶展开(为什么用傅立叶?这就是傅立叶级数的好处,对偶性,得到的是正余弦变换)得到
$$g(\tau)=\frac2\pi + \frac4\pi\sum_{m=1}^\infty \frac{1}{1-4m^2}cos(m\tau)=\frac{4}{\pi}\sum_{m=1}^\infty \frac{1-cos(2m\tau)}{4m^2-1}$$
由于$\Bbb E[\phi(\boldsymbol x)\phi(\boldsymbol y)] = k(\boldsymbol x,\boldsymbol y)$,积化和差后有$\Bbb E[cos(\boldsymbol w \cdot (\boldsymbol x - \boldsymbol y))]=K(\boldsymbol x- \boldsymbol y)$,带入上式,得到了我们需要的核函数关联:
$$\Bbb E[h(\boldsymbol u) \ne h(\boldsymbol v)] = \frac8\pi^2\sum_{m=1}^\infty \frac{1-K(m \boldsymbol u-m \boldsymbol v)}{4m^2-1}$$
这里的最大好处是等式右边是加性核函数$K(\boldsymbol x,\boldsymbol y)$的形式,也就说我们可以通过调节$\sigma$得到任意距离尺度下的LSH。这里[code]有我的代码实现。
总结
这里介绍了四种LSH方法,最原始的Sable Distribution的投影LSH,满足cosine距离的随机超平面投影LSH,以及他的文本特征改进SimHash,最后介绍了RBF kernel下的LSH,基本可以满足我们的需要。当然kernel LSH还会随着kernel map技术的发展而发展,现在有了不错的显示映射方法,比如Efficient Additive Kernels via Explicit Feature Maps,提供了一种有限维有损的显示映射方法,但是值域并不是均匀分布的,需要额外小心。另外一些方法就是有监督的或半监督的,随着应用场景不同而改变,这两年CVPR里有很多此类LSH方法的文章,看来还是比较受欢迎的。Spectral Hash用过一下,感觉效果不好,估计是因为距离度量不适合使用的样本。其实LSH问题的关键是根据数据集和需要度量的相似度,选择合适的menifold进行投影,也算是menifold learning的一个思想吧。